Cheops pi og talmanipulationer, 2. del

af Per Andersen

1. Indledning. Målsætning. Det ægyptiske samfund. Matematikken i Ægypten.
2. Pyramide-mystikken. Konlusioner. Noter. Kildehenvisninger og litteraturfortegnelse.

Pyramide-mystikken

Begynder man at kikke på den litteratur, der er skrevet til forsvar for den mystiske matematik i pyramiderne , overvældes man hurtigt! Desværre overvældes man ikke på grund af argumenternes klarhed og styrke, men derimod af forvirring! I værkerne om pyramidemystikken bliver der regnet over stok og sten. Der bliver nedrundet, oprundet og afrundet. Der bliver indført nye måleenheder. Og hvad der besværliggør studiet af emnet: Kildehenvisninger er lige så sjældne som isvafler i helvede.

Som en af mystik-tilhængerne skriver det:

“Enhver teori om den store pyramide forsøger enten at tyde dens mysterium for i sidste instans at få bekræftet, at pyramiden understreger Bibelens sandheder og præcise udsagn – eller den bestræber sig på at stadfæste, at Keops-pyramiden var både en faraos gravsted og et monument for ham. I første tilfælde bruges pyramidens mål som støtte for teorien, og i sidste har målene (hvis de overhovedet nævnes) kun været noget rent praktisk; man undgik bevidst enhver tolkning eller korrelation. I begge tilfælde efterlader teorierne en forvirret eller dybt respektfuld læser. Ærefrygten gælder pyramidens vældige dimensioner og hvad det mon alt sammen kan betyde; men samtidig bombarderes læseren med forvirrede fortegnelser og registre, vinkler og andre mål, der får ham eller hende til simpelthed at springe dem over i stedet for at beskæftige sig mere med dem.” (25).

Hvorefter han for øvrigt selv går videre med beregninger, der kan forvirre selv den mest hærdede matematiker.

På trods af dette vil jeg i det følgende forsøge at gøre rede for nogle af de mest almindelige matematiske forhold, der påstås at være mystiske ved pyramiderne. Det drejer sig hovedsagelig om forhold ved “den store pyramide” (Kheops). Jeg gør ikke krav på, at listen er komplet, eller at alle relevante kilder er undersøgt – faktisk ved jeg, at dette ikke er tilfældet. Men der er på området så megen litteratur, at udarbejdelsen af en komplet liste over påståede mystiske matematiske forhold ved pyramiderne næsten ville være en livsopgave.

Den følgende liste indeholder en række eksempler på almindelige og typiske påstande vedrørende pyramidernes matematik.

1) Pyramidernes orientering.

Selve orienteringen af pyramiderne mod Nord, er et emne, der ligger på grænsen til at være matematisk. Alligevel er emnet medtaget i denne liste.

Det har været hævdet, at pyramidernes sider er orienteret præcist mod Nord og Øst. Dette er dog ikke korrekt, idet pyramidernes nordrettede sider afviger fra geografisk Nord med vinkler af størrelsesorden 10 minutter. Den pyramide, hvis side er tættest på at være rettet mod Nord, er Kheops-pyramiden, og der vil derfor blive koncentreret om denne i det følgende.

Charroux fastsætter den store pyramides afvigelse fra Nord til at være 4 minutter og 35 sekunder, og han mener dette er usædvanlig nøjagtigt. Som argument anfører han, at observatoriet i Paris afviger fra Nord-retningen med 18 grader (26).

Nu tror jeg nok, at jeg kan finde masser af bygninger, der afviger lige så meget fra Nord-retningen!

For det første er det jo en forudsætning, at Paris-observatoriet faktisk er forsøgt rettet mod geografisk Nord, og for det andet er det en forudsætning, at der er udvist en vis nøjagtighed ved bygningen. Dette har Charroux ikke gjort rede for. Men hvorom alting er, så er en afvigelse på 4 minutter og 35 sekunder faktisk så minimal, at det er usædvanligt.

Andre har så forsøgt at give en forklaring på den minimale afvigelse fra Nord, idet man er gået ud fra, at Kheops-pyramiden oprindeligt har været orienteret præcist mod Nord.

Et aspekt, der har betydning her, er kontinentaldriften (kontinentaldriften er kontinenternes indbyrdes bevægelse igennem tiderne). Ganske vist er denne drift ubetydelig, men når det drejer sig om tidsrum på tusinder af år (som det jo gør i dette tilfælde), så får den dog en betydning. For at forstå dette kan man forestille sig kontinenterne svømmende på en stor kugle. Kontinenterne vil da drive lidt i forhold til hinanden, og hvad der er væsentlig i denne forbindelse er, at de vil drive i forhold til nordretningen. Dette har dog kun betydning over store tidsrum – over flere tusinde år.

Det er imidlertid beregnet, at kontinentaldriften kun kan forklare omkring 1/40-del af Kheops-pyramidens afvigelse fra Nord-retningen (27).

Dette har fået nogle til at spekulere på, at hvis kontinentaltdriften skal forklare hele afvigelsen fra Nord-retningen, så må pyramiderne være betydelig ældre end antaget. Man har beregnet, at Kheops-pyramiden så må være omkring 180.000 år! Dette kræver dog, at pyramiden oprindeligt har været orienteret præcist mod Nord, og at der har været konstant kontinentaldrift igennem tiderne – hvilket dog ikke er tilfældet. Men selv om kontinentaldriften har svinget igennem tiderne , så skulle man kunne konkludere, at Kheops-pyramiden er særdeles meget ældre end normalt antaget (28).

Ser vi nu på, hvordan pyramiderne ved Giza faktisk er orienteret i forhold til Nord, kommer vi frem til følgende tal (29):

• Kheops-pyramiden er orienteret 3 minutter og 6 sekunder vest for nord.
• Khefrens pyramide er orienteret 5 minutter og 26 sekunder vest for nord.
• Mycerinus pyramide er orienteret 14 minutter og 3 sekunder øst for nord.
• Den “sammen-styrtede” pyramide er orienteret 9 minutter og 12 sekunder vest for nord.
• Den lille pyramide er orienteret 10 minutter og 12 sekunder vest for nord.
• Maydoum pyramiden er orienteret 24 minutter og 25 sekunder vest for nord.

Det er korrekt, som det ses, at pyramiderne er orienteret ret præcist mod nord, og der er ingen tvivl om, at ægypterne bevidst forsøgte at rette pyramiderne mod en retning svarende til geografisk Nord. Men der er intet, der tyder på, at pyramiderne oprindeligt har været orienteret præcist mod nord. Det er naturligt at antage, at der ved pyramidebyggeriet – som ved alle andre byggerier – er været en lille fejlorientering.

Derfor er der klart heller ingen argumenter for, at en afvigelse fra Nord svarende til kontinentaldriften, skulle gøre pyramiderne meget ældre end de er. Det er rent gætteri. Endvidere er der jo den lille hage ved kontinentaldrift-teorien, at der er relativ stor forskel på de forskellige pyramiders fejlorientering. Hvis kontinentaldriften skulle forklare alle afvigelserne (altså alle pyramiderne blev bygget med en side rettet præcist mod nord), så måtte der være stor afvigelse i alderen også. Hvis Kheops-pyramiden f.eks. blev bygget for ca. 180.000 år siden, så skulle Khefren-pyramiden være bygget for ca. 300.000 år siden og Maydoum-pyramiden for 1.400.000 år siden. Det vil sige, at Kheops-pyramiden og Maydoum-pyramiden blev bygget med et mellemrum på 1.220.000 år. Tanken virker temmelig absurd!

Hvordan pyramiderne blev orienteret med den relativ nøjagtige Nord-retning, er stadig et åbent spørgmål. Men der er fremkommet forskellige gode, videnskabeligt underbyggede teorier om dette. Disse indbefatter bl.a., at stjernerne eller solen skulle være brugt til orienteringen (30). Man må jo huske på, at ægypterne ikke kendte til kompasset. Der er dog heller ikke her – når man tager i betragtning, at pyramiderne faktisk ikke er rettet præcist mod Nord -grund til at antage, at det ikke skulle have været muligt for ægypterne at orientere pyramiderne på denne mådeDer er tale om godt håndværk, men ikke umuligt håndværk!

Til gengæld er der et andet faktum, der er forbigået af mystikerne. Af ovenstående tabel fremgår det, at pyramiderne med en enkelt undtagelse alle er orienteret lidt vestlig for Nord. Dette kan jo næppe være tilfældet, hvis afvigelserne skal tilskrives tilfældige unøjagtigheder ved bygningen. Men også her er der en rimelig forklaring, der går ud på, at ægypterne har orienteret pyramiderne på bestemte tidspunkter af året – i overensstemmelse med teorien om, at pyramidebyggeriet kun blev foretaget i bestemte perioder af året. Hvis man f.eks. har brugt solen til at orientere siden efter , ville der derved være opstået en systematisk fejl (31).

Så vi kan konkludere, at hverken den forholdsvise præcise orientering mod Nord eller den manglende orientering mod præcis Nord, giver noget reelt grundlag for pyramide-mystikken.

2) Højden af Kheops-pyramiden i forhold til afstanden til solen.

Det hævdes, at højden af pyramiden ganget en milliard præcis er afstanden til solen. Når man hører dette , så synes man, at dette da må være let at bekræfte eller afkræfte. Desværre er det ikke så simpelt som det lyder.

Hvis vi starter med højden af Kheops-pyramiden, så møder vi de første problemer. Højden i dag er på grund af erosion og fjernelse af pyramidens top ikke lig med den oprindelige højde, hvorfor den oprindelige højde jo ikke lader sig måle præcist. Men heller ikke højden i dag er det tilsyneladende let at måle – sikkert på grund af usikkerhed om, hvorfra og hvortil man egentligt skal måle. Den nuværende højde anslås til at være 137,3 meter (32), mens angivelserne af den oprindelige højde varierer fra 146,2 (33) over 146,8 (34), 147,2 (35) og 147,9 (36) til 148,2 meter (37).

Regner man imidlertid med, at højden har været et “pænt” tal i datidens måleenheder, er det nærmeste vi kan komme 280 cubit (en af datidens måleenheder). Dette svarer til 146,7 meter.

Også jordens afstand til solen er der problemer med. Som bekendt beskriver jordens bane om solen ikke en cirkel, men derimod en elipse, og man kan derfor ikke tale om en fast afstand. Regner man med middelafstanden får man en afstand på 149,4 millioner km (38).

Sammenlignes disse to tal, 146,7 og 149,4, finder man, at de absolut ikke er ens. Faktisk er der en afvigelse fra middel-solafstanden på 1,8%.

Pyramidens højde gange en milliard og solafstanden er altså ikke ens – de er ikke engang så tast ved hinanden, at tilfældighed kan udelukkes.

3) Omkredsen af Kheops-pyramidens base ved jorden, divideret med 2 gange højden, giver tallet pi (39).

Denne regel forekommer underligt nok også på formen: Arealet af grundfladen divideret med to gange højder. giver pi (40). Dette sidstnævnte forhold giver ikke pi, som Wilson også ganske rigtigt gør opmærksom på (41). Men da der er tale om et forhold imellem et areal og en længde, er dette forhold afhængigt af måleenheden, og man skal derfor ikke gøre sig forhåbninger om at forholdet pi opstår – men selvfølgelig kan man afpasse enhederne, således at pi faktisk dukker op! Hen lad os se på den rigtige påstand.

En pyramides facon eller form er fuldstændigt bestemt af dens højde og længden af en af siderne. Det er derfor interessant at ser om dette forhold ved Kheops-pyramiden er relateret til pi, for så bestemmer pi jo pyramidens facon (men dog ikke dens absolutte størrelse).

Eftersom der er flere forskellige værdier for den oprindelige højde (se det foregående punkt) og forskellige værdier for længden af pyramiden, kan man, ved at kombinere disse, få adskillige værdier frem. Lad os se på nogle af disse.

Man kan få en meget nøjagtig værdi af pi frem ved at sætte højden lig 146,7 meter, som fundet under sidste punkt og den gennemsnitlige sidelængde lig 230,43 meter (42). Herved giver det ovenstående forhold 3,1415 mens den afrundede værdi for pi er 3,1416!

Men denne værdi for længden er faktisk ikke målt, men beregnet ud fra, at sidelængden skal være 440 cubit sammenholdt med en teoretisk værdi for denne enhed “cubit” (43). Bruger vi værdierne for de målte længder af siderne, får vi en gennemsnitslængde for Kheops-pyramiden på 230,36 meter. Med denne værdi giver forholdet 3,1406.

Endelig kan vi gå tilbage til ægypternes egen enhed “cubit” og beregne forholdet med højden sat til 280 cubit og sidelængden sat til 440 cubit. Dette giver et forhold på 3,1429.

Her har vi tre værdier , der alle ligger lige omkring pi, og med en maksimal afvigelse fra pi på 0,042%. Dette ligner tilsyneladende ikke en tilfældighed.

Ovenstående underbygges også af et andet faktum. Da Herodot (den græske historie-skriver) besøgte Ægypten nogle hundrede år før vor tidsregning, fik han af de ægyptiske præster at vide, at Kheops-pyramiden blev konstrueret, så arealet af en af siderne er kvadratet på pyramidens højde (44) . Hvis pyramiden bliver konstrueret på denne måde, ja så vil omkredsen divideret med to gange højden faktisk altid blive meget tæt ved pi!

Her ser det altså ud til, at der virkelig er indfældet en universel konstant i pyramiden. Spørgsmålet er så: Kunne Ægypterne konstruere Kheops-pyramiden på denne måde? Ja, det tyder vores viden på. Det er jo ikke sikkert, at værdien pi bevidst er indfældet som konstant i pyramiden. Den ovenfor nævnte byggemåde ville jo af sig selv give et sådan forhold.

Hvis endelig ægypterne bevidst brugte værdien pi, så er det jo heller ikke sensationelt. Vi har jo i sidste afsnit set, at ægypterne faktisk godt kendte en værdi for pi, nemlig 3,1605. Den i pyramiden forekommende værdi for pi ser dog ud til at være nøjagtigere end 3,1605. Dette tyder på, at pyramidens pi-værdi er opstået på den indirekte måde, altså ved at arealet af en side skulle være kvadratet af højden.

4) Kheops-pyramidens højde i forhold til jordens radius er lig Kheops-pyramidens omkreds i forhold til jordens omkreds.

Denne påstand er set fremsat af Chatelain (45). Foretages en efterregning fås følgende: Vi bruger værdien 146,7 meter for højden på Kheops-pyramiden og jordens middelradius sættes til 6367 km (46). Dette giver et forhold mellem højde og radius på 23,04 (divideret med 1 million).

Bruger vi nu værdien 23 0,56 meter for sidelængden og omkredsen af jorden sættes til 40076 km (47), får vi forholdet 922,24 meter divideret med 40076 km, hvilket er 23,01 (divideret med 1 million).

Her har vi tilsyneladende fundet en nøje overensstemmelse mellem pyramidens og jordens dimensioner! Det kunne ægypterne da ikke vide – eller kunne de? Nej, det kunne de ikke. Eksemplet her er til gengæld et glimrende eksempel på, hvordan man kan snyde med talmæssige manipulationer!

Antages nemlig, at det foregående punkt 3 er korrekt. Så fås, at omkredsen af pyramiden divideret med 2 gange højden giver pi. Det vil sige, at omkredsen divideret med højden giver to gange pi. Ser vi nu på jorden, så må vi huske på, at den tilnærmet er en kugle. Og det betyder, at jordens omkreds divideret med radius også giver to gange pi. Nu har vi med andre ord fundet et forhold i Kheops-pyramiden, der giver pi, og vi har fundet ét andet forhold ved Jorden, der også giver pi. Gængse regneregler siger nu, at man kan “bytte rundt” med faktorerne. Således giver almindelig forholdsregning nu ovenstående postulat!

Denne “mystiske” sammenhæng imellem pyramiden og jorden, beror altså fuldstændig på det forhold, der er skitseret under punkt 3.

5) Hvorfor Kheops-pyramiden hælder 52 grader.

Følgende bliver anført: Antag at pyramiden blev bygget på et tidspunkt, hvor jordens hældning var 22 1/2 grader, og at pyramiden befandt sig på 29 1/2 grads bredde. Dette forklarer da hældningen af Kheops-pyramiden på 52 grader, idet solens stråler da ville stå vinkelret på pyramide-siden ved vintersolhverv (48). Se figur 3.

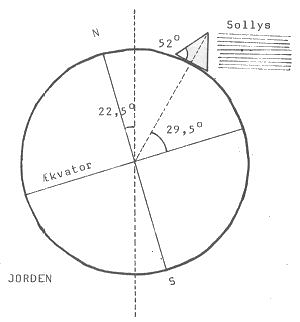
Fig. 3.

For det første er Kheops-pyramidens hældning ikke 52 grader, men derimod 51 grader og 52 minutter. Men så kunne man jo blot antage, at pyramiden blev bygget på et tidspunkt, hvor Jordens hældning var 22 grader og 2 minutter! Essensen er at det er den rene og skære gættekonkurrence. Man kan få et hvilket som helst tal (hældningsvinkel) frem, ved at blot at lægge to andre tal sammen. Argumentet er absurd!

6) Forholdet 3:4:5 i Khefren-pyramiden.

Det bliver påstået, at forholdet imellem den halve grundlinie, højden og kanten (afstanden fra toppen til midtpunktet af en side) af Kefren-pyramiden er 3:4:5. Bruger vi kildens mål på 107,625, 143,5 og 179,375 (49), bliver forholdet faktisk nøjagtig 3:4:5. Bruger vi tallene fra en anden kilde, f.eks. en halv grundlinie på 107,75 meter og en højde på 143,67 meter, bliver forholdet ikke helt 3:4:5, men stadigvæk så tæt på, at det nok ikke er tilfældighed.

Altså er det nok ikke nogen tilfældighed at pyramiden blev bygget med dette forhold. Men hvad vil det egentlig sige. Det vil jo sige, at ægypterne byggede forholdet imellem den halve side og højden som 3:4. Dette kunne være en tilfældighed, men ægypterne kunne også have vist, at dette automatisk ville medføre et forhold til kanten på 3:4:5. Der er intet, der tyder på, at en sådan viden ikke var til stede i Ægypten på daværende tidspunkt.

Man kender mange andre “rene” forhold i pyramidernes mål. F.eks. kendes fra Kheops-pyramiden forholdene 1:2 og 10:11.

7) Rumfanget af en bestemt sten er et multiplum af pi.

Så dukker konstanten pi op nok engang. Denne gang findes rumfanget af den store granitplade i Kheops-pyramidens kongekammer-forværelse. Stenens mål findes til at være 48,57 fod, 15,7 fod og 41,2 fod, hvilket giver et rumfang på 31417 kubikfod (50). Dette er besnærene tæt ved den rigtige værdi for pi, men også denne gang er det nødvendigt at tænke sig om to gange inden der konkluderes noget.

Hvad nu, hvis stenen var blevet målt i meter? Ja, så ville målene have været 14,81 meter, 4,79 meter og 12,57 meter, hvilket giver et rumfang på 891,71 kubikmeter. Og dette tal har jo intet med pi at gøre! Årsagen til dette nye aspekt er, at vi nu ikke længere beskæftiger os med forholdet mellem f.eks. to længder, men med absolutte størrelser. Dette betyder, at enheden har betydning for det resultat man kommer frem til.

Af ovenstående kan man altså slutte, at enten er det en tilfældighed, at denne sten har det anførte rumfang i kubikfod (der er jo mange sten i en sådan pyramide!), eller også kendte ægypterne den måleenhed, der ville blive brugt årtusinder senere i England. Hvad er mest sandsynligt?

Fig. 4: Arabere på vej op ad det store galleri i Cheops-pyramiden.

8) Antal dage i året er fundet adskillige steder i Kheops-pyramidens mål.

Antallet af soldøgn i et år er afrundet 365,242 (det tropiske år). Dette svarer til et skudår cirka hvert fjerde år. Dette tal menes fundet i overflod i pyramiden. Man anfører (51):

1. Afstanden fra midten af Kheops-pyramiden til 35. stenskifte på pyramiden (den horisontale afstand) er 3652,42.
2. Sidelængden (9131 pyramidetommer) divideret med 25 pyramidetommer giver 365,24.
3. Kongekammerets længde plus halvdelen af forværelsets længde er 365,24.
4. En cirkel med forværelsets længde (116,25 pyramidetommer) som diameter har en 365,24 tommer omkreds.
5. Kongekammerets bredde (206 ,066 pyramidtommer) gange med kvadratroden af pi giver 365,24.
6. Kongekammerets dobbelte længde (2 x 412,12 pyramidetommer) målt hen ad Galleriets gulv, har på denne distance en 365,24 tommers stigning fra vandret.
7. De fire sidelinjers samlede antal pyramidetommer svarer til et århundredes døgn.
8. Det 35. stenskiftes omkreds i pyramidetommer svarer til dagene i 80 solår.

Ved påstand nummer 1) mangler totalt en angivelse af måleenheden, så argumentet er uden værdi.

Med hensyn til 2), så er det korrekt at 9131 divideret med 25 er lig med 365,24. Men 9131 pyramidetommer svarer til 231,93 meter, idet 1 pyramidetomme svarer til 2,54 cm, og dette er jo ikke pyramidens længde – den gennemsnitlige sidelængde er 230,43 meter. Sidelængden svarer altså til 9069 pyramidetommer.

Ser vi på punkt 3), så skulle kongekammerets længde være 412,12 ifølge 6) og halvdelen af forværelsets længde skulle være 58,125 ifølge 4). Dette giver tilsammen 470,245 – noget langt fra 365,24.

Med hensyn til 4), så giver cirklens omkreds 365,21 og ikke 365,24 pyramidetommer. Der er dog kun en minimal afvigelse.

Foretager man udregningen angivet i punkt 5), så får man faktisk tallet 365,24.

Galleriet stiger i forholdet 1:2 (52), så stigningen på længden 2 x 412,12 vil faktisk være 412,12 og ikke 365,24 som påstået i 6.

Udsagnet i 7) siger præcis det samme som 2), blot med andre ord. Altså heller ikke korrekt.

Endelig er der 8), der ikke er mulig at kontrollere med de opgivne data.

Alt i alt må man sige, at overfloden er svundet noget ind. Af de 8 påstande er kun 2 tilnærmelsesvis korrekte.

Man lægger mærke til, at der optræder en ny måleenhed: Pyramidetommen. Var det en måleenhed ægypterne brugte? Nej, det var faktisk en enhed, som Smyth indførte, da han opmålte den Store Pyramide (53). Og eftersom den er efter Smyth’s behag, så er det ikke underligt, at han kunne få nogle af målene til at passe med en konstant som 365,24! Der er jo nemlig igen tale om absolutte længder, hvor måleenheden har altafgørende betydning.

Man skal også være klar over, at antallet af soldøgn i et år kan udregnes på flere forskellige måder. Det her anvendte “tropiske år” har en værdi på 365,242. Bruger man andre definitioner af “året” kan man få andre værdier frem, deriblandt 365,256, 365,255, 365,259 og 346,620. Der er med andre ord en mængde muligheder – så passer pyramidetallene ikke med den ene værdi, så kan man jo altid forsøge med en af de andre!

Med andre ord er der i ovenstående ikke bevis for andet, end at det er let at manipulere med tal (og læseren).

Fig. 5: Diorite statue af Khefren (fra 6. dynasti).

9) Konstanten pi – nok engang.

Denne gang hævdes det, at den optræder i følgende to tilfælde ved Kheops-pyramiden (54):

1. Kongekammerets længde adderet til dets højde og divideret med bredden giver pi.
2. Kongekammer-sarkofågets længde og bredde divideret med dens højde giver pi.

Efterprøves først påstand l) finder vi, at kongekammeret måler 10,46 x 5,82 (højden) x 5,23 meter (55). Udregnes nu længden plus højden divideret med bredden, fås 3,1128, mens pi som bekendt afrundet er 3,1416.

I det andet tilfælde opgives sarkofagens mål til ca. at være 7,5 x 3 x 3,5 (højden). Udregnes her længden plus bredden divideret med højden, fås 3,0000.

Man må vist konstatere, at ingen af de to påstande er særlig overbevisende.

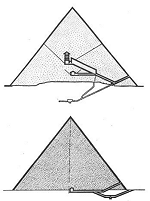
Fig. 6: De indre ganges forløb i Cheops-pyramiden (øverst) og Khefren-pyramiden (nederst).

10) Nonsens!

Under denne overskrift gemmer sig et par eksempler på udsagn eller påstander der simpelthen ikke giver nogen mening (56):

1. En af Kheops-pyramidens sideflader repræsenterer en kurvet fjerdedel af den nordlige halvkugle.
2. Pyramidens top svarer til Nordpolen, mens omkredsen af basis svarer til Ækvator.

Det er muligt, at forfatteren har ment noget med disse påstande (det modsatte er også muligt). Men i så fald, har han i hvert fald formuleret sig yderst dårligt, eller også har oversætteren totalt misforstået noget.

Denne gennemgang viser med al tydelighed, at de såkaldte “pyramide-mysterier”, der har relation til matematik, for en stor del består af manipulationer på manipulationer og unøjagtigheder på unøjagtigheder. Den kerne af fakta, der bliver tilbage lægger bestemt ikke op til, at der skulle avanceret matematik til at bygge pyramiderne.

Konklusioner

Vi har set, at det ægyptiske samfund var temmelig stabilt. Dette gælder også for matematikken, der var udviklet til et vist trin, men som aldrig rigtig nåede videre.

Fra forskellige matematiske kildetekster vides, at ægypterne kendte metoder til at beregne en pyramides hædningsvinkel og rumfang, samt en stubpyramides rumfang. Endvidere er der en række eksempler på udregninger af pyramiders hædningsvinkler. Både det forhold, at disse eksempler beskæftiger sig med hældningsvinkler, der ligger tæt ved Giza-pyramidernes, og det forhold, at de øvrige talopgivelser i eksemplerne gælder pyramider af omtrent samme størrelse som f.eks. Kheops- og Khefren-pyramiderne, viser, at de matematiske skrivere faktisk beskæftigede sig med beregninger over konkrete ægyptiske pyramider.

Matematiske kildetekster viser også, at ægypterne faktisk godt kendte en værdi for pi, eller at man rettere sagt havde formler for beregning af f.eks. cirklens omkreds. Den værdi for pi man benyttede sig af, ligger relativt tæt ved den rigtige værdi, når man tager datidens forhold i betragtning.

De personer der mener , at pyramiderne indeholder avanceret matematik, prøver at bevise dette ved en lang række forhold i pyramiderne. Går man disse forhold nærmere efter, viser det sig, at de fleste kan tilskrives ikke-mystiske forhold eller på anden måde afvises. Blandt de fejl mystikerne gør er at indføre egne enheder eller bruge nutidige enheder ved eksempler, der er afhængige af måleenheden – f.eks. hvor et mål skal svare til at antal dage.

Andre eksempler arbejder med forhold mellem samme type størrelser, og undgår derved problemerne med måleenheden. Men her begår man så andre fejl. Han påstår, at størrelser er lig hinanden, selv om faktiske udregninger viser, at dette ikke er korrekt. I tilfælde, hvor to værdier ligger tæt ved hinanden, kan tilfældighed sjældent udelukkes. Eller fejlen opstår på kryptisk vis, som med eksempel 4 i sidste afsnit – dette gøres nok ikke bevidst, men det illustrerer glimrende disse forfatteres manglende kritiske sans ved bearbejdelse af stoffet.

Tilbage er enkelte forhold, der kan stå for en nærmere undersøgelse. I denne gennemgang er der fundet 2 sådanne forhold.

Det viser sig, at Kheops-pyramidens base ved jorden, divideret med 2 gange højden, tilnærmelsesvis giver tallet pi. I sig selv er dette ikke revolutionerende, idet ægypterne godt kendte en tilnærmet værdi for pi. Men den værdi for pi pyramiden udtrykker er langt mere nøjagtig end den i kilderne fundne værdi. Dette støtter oplysningen fra Herodot om, at Kheops-pyramiden er bygget, så arealet af hver side er lig kvadratet på højden -dette giver automatisk pi-forholdet. Der var ikke andre af de påståede forekomster af konstanten pir der kunne stå for en mere nærgående undersøgelse.

Et andet forhold, der kan stå for en nærmere undersøgelse, er forholdet 3:4:5 i Khefren-pyramiden. Dette forhold fremkommer imellem den halve grundlinie, højden og kanten (afstanden fra toppen til midtpunktet af en side).

Denne kerne af matematisk indhold i pyramiderne ligger absolut inden for rammerne af vores opfattelse af matematikken i oldtidens Ægypten.

Denne rapport gør ikke krav på at have foretaget en fuldstændig analyse af dette emne – dette er umuligt ved et studie på få måneder. Centrale og typiske eksempler ved pyramiderne er dog udvalgt og undersøgt, og disse giver ingen støtte til pyramidemystikken.

Konklusionen af dette må derfor være: I denne undersøgelse, hvor centrale og typiske eksempler på påståede mystiske, matematiske egenskaber ved de klassiske pyramider i Ægypten er taget op til nærmere undersøgelse, er der ikke fundet bevis for, at pyramidematematikken ikke er konsistent med det daværende ægyptiske samfund.

Noter

1. Se (Gardner, 1977), p 82.
2. Se (Spigel, 1973) og (Wilson, 1978), p 85f.
3. Se (Smith, 1977), p 203.
4. Se (Gardner, 1977), p 86.
5. Oplysningerne i dette afsnit stammer hovedsagelig fra (Holm-Rasmussen, 1980), der er et nyere dansk værk om ægyptologien. Værket beskæftiger sig med den ægyptologiske forskning, som bl.a. er udført af E. Horning og H. Schäfer, og indeholder adskillige nyere forskningsresultater.
6. Se (Brier, 1977), p 31f.
7. Se (Edwards, 1947), p 13.
8. Se (Däniken, 1969), p 89 og p 98.
9. Kronologien er baseret på (Holm-Rasmussen, 1980) og (Toth, 1980).
10. Se (Waerden, 1954), p 16.
11. Se (Gillings, 1972).
12. Se (Neugebauer, 1957), p 78.
13. Se (Waerden, 1954), p 16.
14. Se (Waerden, 1954), p 16.
15. Se (Waerden, 1954), p 17.
16. Se (Gillings, 1972), p 185.
17. Se (Gillings, 1972), p 185.
18. Se (Gillings, 1972), p 185.
19. Se (Gillings, 1972), p 187.
20. Se (Brier, 1977), p 38 og (Wilson, 1978), p 131f.
21. Se (Waerden, 1954), p 32.
22. Se (Waerden, 1954), p 32.
23. Se (Neugebauer, 1957), p 78.
24. Se (Neugebauer, 1957), p 72.
25. Se (Toth, 1980), p 113.
26. Se (Charroux, 1969), p 62.
27. Se (Svendsen, 1977), p 218f.
28. Se (Svendsen, 1977), p 218f.
29. Se (Svenonius, 1936), p 3f.
30. Se (Svenonius, 1936), p 3.
31. Se (Svenonius, 1936), p 3.
32. Se (Toth, 1980), p 115.
33. Se (Paulsen, 1980), p 63 og (Chatelain, 1980), p 65.
34. Se (Wilson, 1978), p 176.
35. Se (Paulsen, 1980), p 63 og (Chatelain, 1980), p 65.
36. Se (Toth, 1980), p 115.
37. Se (Charroux, 1969), p 62.
38. Se (Charroux, 1969), p 62.
39. Pi er forholdet imellem en cirkels omkreds og diameter. Her bliver alle værdier for pi angivet afrundet til 5 cifre.
40. Se f.eks. (Däniken, 1969), p 86.
41. Se (Wilson, 1978), p 176.
42. Se (Toth, 1980), p 115.
43. Se (Paulsen, 1980), p 68.
44. Se (Toth, 1980), p 123.
45. Se (Chatelain, 1980), p 66.
46. Se (Gyldendals Tibinds Leksikon, 1978).
47. Se (Gyldendals Tibinds Leksikon, 1978).
48. Se (Chatelain, 1980), p 70.
49. Se (Chatelain, 1980), p 74.
50. Se (Toth, 1980), p 122.
51. Se (Toth, 1980), p 122f og 125.
52. Se (Paulsen, 1980), p 51.
53. Se (Toth, 1980), p 125.
54. Se (Toth, 1980), p 126.
55. Se (Paulsen, 1980), p 54.
56. Se (Toth, 1980), p 126

Kildehenvisninger og litteraturfortegnelse

(Borchardt, 1922)	Borchardt, Ludwig. Gegen die Zahlenmystik an der grossen Pyramide bei Gise. Behrend & Co., Berlin, 1922.
(Brier, 1977)	Brier, Bob. En pilgrimsfærd i det 20. århundrede. I Martin Ebon (red.): Pyramider og pyramidekraft. Sphinx og Nihil, Haderslev, 1977.
(Charroux, 1969)	Charroux, Robert. Mysterier i 100.000 år. Strubes Forlag, Viborg, 1969.
(Chatelain, 1980)	Chatelain, Maurice. Our Ancestors came from Outer Space. Arthur Barker Limited, London, (1980).
(Cottrell, 1956)	Cottrell, Leonard. The Moutains of Pharaoh. J. Hale, London, 1956.
(Davidson, 1932)	Davidson, D. & Aldersmith, H. The Great Pyramid, its Divine Message. Williams & Norgate, London, 1932.
(Däniken, 1969)	Däniken, Erich von. Fortids Gåder … Fremtids Virkelighed. Strubes Forlag, Viborg, 1969.
(Edgar, 1910)	Edgar, John & Edgar, Morton. The Great Pyramid Passages and Chambers. Glasgow, 1910.
(Edwards, 1947)	Edwards, I.E.S. The Pyramids of Egypt. London, 1947. På dansk: Ægyptens Pyramider. Gads Forlag, København, 1961.
(Gadow, 1973)	Gadow, Gerhard. Fortids Gåders Forklaring. Nihil, Haderslev, 1973.
(Gardiner, 1961)	Gardiner, Alan. Egypt of the Pharaohs. Oxford University Press, Oxford, 1961.
(Gardner, 1977)	Gardner, Martin. Litteratur om den store pyramide. I Martin Ebon (red.): Pyramider og pyramidekraft. Sphinx og Nihil, Haderslev, 1977.
(Gillain, 1927)	Gillain, O. La Science Egyptienne. L’arithmetique au Moyen Empire. Brussels, 1927.
(Gillings, 1972)	Gillings, Richard J. Matematics in the Time of the Pharaohs. The MIT Press, (1972).
(Herodot, 1897)	Herodot. Historie 1-2. København, 1897.
(Holm-Rasmussen, 1980)	Holm-Rasmussen, Torben. Det gamle Ægypten. Berlingske Forlag, Viborg, 1980.
(Mendelssohn, 1974)	Mendelssohn, Kurt. The Riddle of the Pyramids. Thames and Hudson, Cambridge, 1974.
(Nuegebauer, 1952)	Neugebauer, O. The Exact Sciences in Antiquity. Princeton, New Jersey,1952.
(Paulsen, 1980)	Paulsen, Hubert. Den store pyramide. Gyldendal, Viborg, 1980.
(Peet, 1923)	Peet, T.E. The Rhind Matematical Papyrus. London, 1923.
(Petrie, 1883)	Petrie, F. Pyramids and Temples of Giza. Field & Tuer, London, 1883.
(Russell, 1891)	Russell, Charles Taze. Studies in the Scripture III. 1891.
(Seiss, 1877)	Seiss, Joseph A. The Great Pyramid: A Miracle in Stone Porter & Coates, Philadelphia, 1877. Genudgivet: Steinerbooks, 1976.
(Smith, 1977)	Smith, Warren. Pyramider verden over. I Martin Ebon (red.): Pyramider og pyramidekraft. Sphinx og Nihil, Haderslev, 1977.
(Smyth, 1864)	Smyth, Charles Piazzi. Our Inheritance in the Great Pyramid. A. Straham & Co., London, 1864.
(Smyth, 1867)	Smyth, Charles Piazzi. Life and Work of the Great Pyramid. Edmonton & Douglas, London, 1867.
(Smyth, 1868)	Smyth, Charles Piazzi. On the Antiquity of Intellectual Man. Edmonton & Douglas, London, 1868.
(Spiegel, 1972)	Der Spiegel. Nr. 12,1973.
(Svendsen, 1977)	Svendsen, Peter Juhl. Den store pyramide – endnu en gang. I Martin Ebon (red.): Pyramider og pyramidekraft. Sphinx og Nihil, Haderslev, 1977.
(Svenonius, 1936)	Svenonius. On the Orientation of the Egyptian-Pyramids. Meddelande från Lunds Astronomiska Observatorium, Ser. II, Nr. 80,1936.
(Taylor, 1864)	Taylor, John. The Great Pyramid: Why Was It Built? And Who Built It? Lougmans, Green, London, 1864.
(Toth, 1980)	Toth, Max. Pyramidernes Gåder. Bogan, Skive, 1980.
(Waerden, 1954)	Waerden, B.L. van der. Science Awakening I. P. Noordhoof Ltd, Groningen, (1954).
(Wake, 1882)	Wake, C. Staniland. The Origin and Significance of the Great Pyramid. Reeves & Turner, London, 1882. Genudgivet: Wizards Booksheif, Mineapolis, 1975.
(Wheeler, 1935)	Wheeler, Noel F. Pyramids and their Purpose. Antiquity 9 (1935).
(Wilson, 1978)	Wilson, Clifford. War of the Chariots. Master Books, California, 1978.

Kilde: Cheops pi og talmanipulationer. Skeptica, 1982. – ISBN 87-8825-00-5