af Isabelle Gauthier og Andrea Ruas, oversat af Harald Fastrup.
- 1. del: Introduktion og historie
- 2. del: Det visuelle system
- 3. del: Kunstneriske illusioner
- 4. del: Optisk-geometriske illusioner
- 5. del: Subjektive konturer
Før vi forsøger at klassificere de optisk-geometriske illusioner, er det vigtigt at definere disse. Disse illusioner fremkaldes af geometriske figurer, der fremkalder fejlbedømmelser af dimensioner, orientering, krumning, retning eller form af visse elementer.
I løbet af anden halvdel af det nittende århundrede, opdagede pionerer indenfor den eksperimentelle psykologi, Delboef, Hering, Müller-Lyer og andre et større antal illusioner, kaldet optisk-geometriske, som de har givet navn til. Man har katalogiseret mere end 200 af disse fænomener.
Man anser traditionelt, at en geometrisk illusion består af to elementer: Et ?induktionselement?, som fremkalder en deformering og et ?test-element?, som underkaster sig. For eksempel, ved Müller-Lyer´s figur, udgør pilespidserne induktions-elementet og de horisontale linier test-elementet. Ved Poggendorff-figuren er de parallelle linier induktions-elementet og de skrå segmenter test-elementet. I løbet af et århundrede har man fremsat forskellige forklaringer på de geometriske illusioner. De mest overbevisende er enslydende, hvad angår tre fundamentale punkter. For det første findes illusionerne i det perceptive område og har intet at gøre med tanke eller ræsonnement. Faktisk ved man godt, at flertallet af de følgende illustrationer er geometriske illusioner, men det forhindrer ikke, at man opfatter fordrejningerne. For det andet opstår illusionerne ikke i nethinden. De udspiller sig, selv om induktions-elementet placeres foran det ene øje og test-elementet foran det andet øje. De opstår derfor i det visuelle system bagved corpus geniculatum laterale, der hvor informationerne for første gang samler sig fra hvert øje. For det tredje skyldes illusionerne ikke øjnenes bevægelser. De opstår i fuldt flor, selv om expositionstiden er for kort til at øjet har tid til at scanne figuren.
A. Klassificering af de geometrisk-optiske illusioner
Hvis man forsøger at klassificere illusionerne som funktion af deformeringerne, bliver det klart, at ingen klassificering er tilfredsstillende, idet alle har været genstand for mange forskellige forklaringer. Ikke desto mindre må man forsøge at klassificere dem summarisk, om ikke andet så for at få en ide om de mange varianter af disse illusioner.
1) Sammenligning af størrelse
Talrige illusions-figurer fremkalder en sammenligning af størrelsen af figurens elementer. Den resulterer oftest i en kontrasteffekt: Den tilsyneladende størrelse af de største elementer overvurderes i sammenligning med de mindste og omvendt. Det tydeligste eksempel er uden tvivl Titchener´s illusion. Man har imidlertid i visse tilfælde henvist til assimilationsprincippet, ifølge hvilket, når forskellene er minimale mellem de største og de mindste elementer, man er tilbøjelig til at bagatellisere disse forskelle. Det resulterer i en sammenligning mellem et test-element og et større induktions-element (hvoraf følger en overvurdering af test-elementet) eller et mindre induktions-element (altså en undervurdering af element-testen).
Titchener´s illusion.
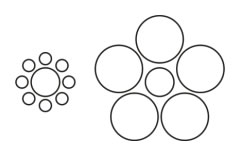 |
Den centrale cirkel i den venstre figur synes større end den centrale cirkel i den højre figur. |
Delboeuf´s illusion.
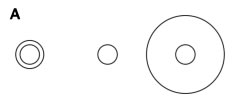 |
a) eksempel på kontrast: Den indre cirkel i den venstre figur synes større end den centrale cirkel, og den indre cirkel i den højre figur synes mindre end cirklen i centrum. |
 |
b) eksempel på sammenligning: Den indre cirkel i den venstre figur synes større end den ydre cirkel i den højre figur. |
2. Rum-opdeling
 |
Et rum, som er delt eller optaget af talrige elementer synes i almindelighed større end et ikke-opdelt rum. Det typiske eksempel er Oppel-Kundt´s illusion |
3. Vertikalitet
En vertikal linie synes længere end en horisontal af samme længde, fordi øjets bevægelser horisontalt er lettere end bevægelser vertikalt. Det hyppigst citerede eksempel er det omvendte T, men det må bemærkes, at denne form giver anledning til ?konkurrence-illusionen? fordi, udover overvurderingen af den vertikale komponent, er der en kontrasteffekt af størrelsen, der fremkaldes af forholdet mellem den vertikale komponent og hvert segment af den horisontale. Man får en ren effekt af vertikaliteten ved at anvende en figur formet som et L.
Vertikalitetens illusion
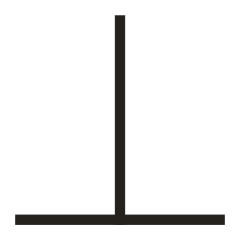 |
I denne figur synes den lodrette streg længere end den vandrette, skønt de har samme længde. |
4. Effekten af vinkler
Illusionerne, der skyldes virkningen af vinkler, er meget talrige og uden tvivl de mest iøjnefaldende. Man anfører to principper for at forklare dem. På den ene side er man tilbøjelig til at overvurdere spidse vinkler og at undervurdere stumpe. Man har kaldt dette Orthogonalitets-princippet , d. v. s. en tendens til at gøre vinkler rette. Dette princip gør det let at forklare Zöllners og Herings illusioner, men det kan også anvendes på Poggendorffs og Müller-Lyers illusioner.Det andet princip drejer sig om at overvurdere siderne i en stump vinkel og at undervurdere siderne i en spids vinkel. I dette tilfælde kan Müller-Lyers illusion tjene som eksempel.
Zöllners illusion
 |
De skrå linier synes ikke parallelle, skønt de er det. De synes deformerede på grund af de små streger, der danner sekundært mønster. |
Herings illusion
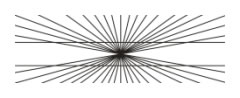 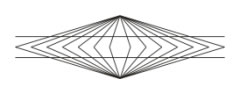 |
De horisontale linier synes bøjede, skønt de er rette og parallelle. |
Poggendorff´s illusion
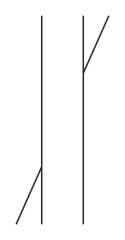 |
De skrå linier synes ikke at flugte, skønt de gør det. |
Müller-Lyers illusion.
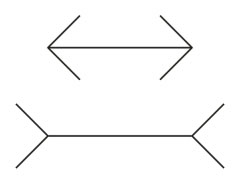 |
Den øverste linie synes kortere end den nederste. |
5. Perspektivet
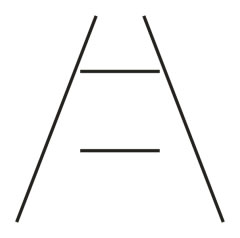 |
Den øverste horisontale linie synes længere end den nederste. Træk, der tydes som perspektiv, giver illusioner om størrelse. Ponzo´s illusion, der kunne betragtes som en illusion angående størrelse, forklares hyppigt som en perspektivisk effekt, lige som Sanders illusion kan betragtes som en perspektivisk illusion, der forestiller et rektangel set fra siden. |
Sanders illusion
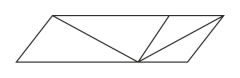 |
Den højre diagonal synes kortere end den venstre, skønt de har samme længde. |
6. Cirkelbuers krumning
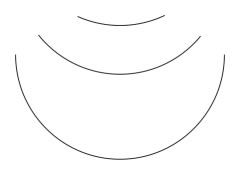 |
Den tilsyneladende krumning af en cirkelbue varierer med buens længde. Kortere buer ses mere flade end lange, selv om krumningen er den samme. |
De tre circelbuer synes at have forskellig krumning, skønt de har samme radius.
B) Opfattelsen af illusioner afhænger af kulturen.
Illusioner afhænger ikke alene af vort synssystem, men også af vor kultur i videste betydning. Således synes Europæere at have en kraftigere Müller-Lyers illusion og en svagere omvendt T illusion end andre etniske grupper, især afrikanske.
Vi, der lever i Vesten i en verden domineret af geometriske former med lige vinkler (beboelser med lodrette linier, vertikale mure, horisontale lofter?) har en kraftig tilbøjelighed til at overvurdere spidse vinkler og undervurdere de stumpe, idet vi tenderer mod at gøre dem rette. Dette er grunden til, at vi er mere følsomme for Müller-Lyers illusion.
Hvad angår det omvendte T´s illusion, er en anden forklaring mulig. Da afrikanerne lever på savannen, som er meget flad og da deres omgivelser er praktisk taget fri for træer, huse og master, er de mindre vant til at bedømme verticale linier. Derfor bliver de lettere narret af det omvendte T´s illusion.
Kilde:www.loginnovation .com/rogerg/illusion /index.html
[*]
[*]

Seneste kommentarer